I 1982 så hobbymatematiker og flyvert, senere purser, Børre Nyhoff en film der astronom Carl Sagan forklarte dimensjoner og geometri. Han ble oppslukt og klarte ikke legge det fra seg. Til tross for at han ikke hadde noen matematisk utdannelse, begynte han å grave i universets geometriske sammenhenger.
Gjennom jobben i SAS hadde Nyhoff mulighet til å besøke forskere i hele verden. Han besøkte Benoît Mandelbrot i New York, mannen som oppdaget fraktaler i matematikk, og fysiker John Ellis på Cern, for å nevne noen. I over 40 år grublet han på geometriske og matematiske sammenhenger. Dette førte til at han på et tidspunkt fant en sammenheng mellom toner og geometri som mange har lett etter. Det er en stund siden Nyhoff fant denne sammenhengen, men i 2023 ble funnet publisert i et matematisk tidsskrift.
Børre Nyhoff
Født i Oslo 31.10.1957, død 21.9.2023.
Han jobbet som flyvert og purser i SAS i det meste av sin karriere. De siste årene jobbet han som manager og prosjektleder i musikkbransjen.
Han hadde tidlig en interesse for musikk, matematikk, geometri og symmetri og var alltid drevet av innovative måter å betrakte universet på.
Underkommunisert skjønnhet
– Mange ser ikke skjønnheten i matematikk, og da tror de at den dreper musikken. Musikk har alltid vært koblet til følelseslivet, og derfor er denne forskningen tung for noen musikere. Matematisk estetikk er noe som ofte blir underkommunisert, sier komponist og pianist Wolfgang Plagge.
Han er en av dem Nyhoff snakket med. Selv er ikke Plagge bekymret for å beskrive musikken matematisk. Historisk har koblingen mellom disse fagene vært mye sterkere enn den er i dag. Musikk spiller en så viktig rolle i vår tilværelse at det faktisk var noe av det første som ble beskrevet matematisk.

Det var Pytagoras som forsto at det finnes noen toner i musikk som harmonerer perfekt med hverandre. Disse kalles oktaver, og disse tonene har to interessante egenskaper til felles. Den viktigste er at det er utgangspunkt for vakker musikk. Den andre er at de består av én enkelt sinuskurve med et enkelt 2:1-forhold i frekvens.
Selv om det har skjedd mye siden Pytagoras levde for 2500 år siden, er det én ting som ikke har skjedd: Ingen har helt klart å koble tonene til geometri, i alle fall ikke som er offentlig kjent.
– Pytagoras hadde ingen forståelse for frekvenser, men han var vanvittig nær uten å vite det, forteller Plagge.
Da Nyhoff presenterte sine ideer for Plagge, var hans første tanke at dette ikke kunne stemme:


– Da jeg møtte ham, tenkte jeg at enten er dette bullshit, eller så blir det virkelig interessant. Han kom med en uhildethet, for det var aldri snakk om å selge noe, men ekte interesse for å forstå sammenhengene, forteller Plagge om deres første møte.
Og det skulle vise seg å bli virkelig interessant. Kunne det være at Nyhoff, som hadde lært seg det han kunne om matematikk på egen hånd, hadde sett en kobling som andre har lett etter siden Pytagoras?
Sinuskurver og toner
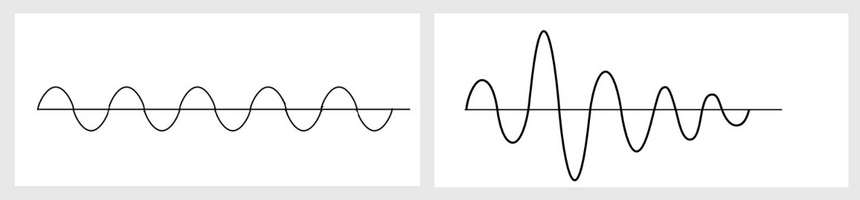
Sinuskurven er en jevn, repeterende kurve beskrevet av funksjonen f(x)= sin x. Rene toner består av én enkelt frekvens. Det betyr at rene toners sinuskurve møter x-aksen samme sted. Sammensatte toner består av flere frekvenser.
– En spesiell henvendelse
I middelalderen var matematikk og musikk to fag som hadde mye til felles. De var begge en del av det som ble kalt «tallkunstens quadrivium». Tallkunstene var regnet som astronomi, aritmetikk, geometri og musikk. Det var anerkjent at disse fagene hang sammen. Derfor var det også mange som forsøkte å finne sammenhenger på tvers av fagene, for eksempel ved å få planetbanene til å følge geometriske figurer eller mønstre. Liknende forsøk ble gjort med musikk.
– På Fysisk institutt får vi ofte mailer fra folk med rare ideer, for eksempel om mørk materie eller teorier om alt. Det er mange som spekulerer på dette, så slike henvendelser får vi fra tid til annen, men henvendelsen fra Nyhoff var spesiell, forteller professor Sverre Holm ved Universitetet i Oslo.
Holm forteller at han ble nysgjerrig på prosjektet, og etter hvert skjønte han at Nyhoff faktisk kunne ha rett. Resultatet ble publisert i tidsskriftet The Mathematical Intelligencer i 2023, like før Børre Nyhoff gikk bort.
.png)
.jpg)
Holm forklarer at han ikke er overrasket over at det er så mange som har ønsket å finne en sammenheng mellom geometri og musikk:
– Disse fagene har vært en del av kjernepensumet siden middelalderen, sier Holm.
Samtidig advarer han om at det ikke er alltid er mulig å tvinge universet inn i bestemte geometriske mønstre eller figurer:
– Kepler ville ha planetbanene til å henge sammen ifølge geometriske figurer, men det gjør de ikke, så det fikk han ikke til, sier Holm.
Tanken om at verden er skapt etter geometrisk perfeksjon er gammel, men dessverre stemmer det ikke alltid. Kanskje er det derfor det har tatt så lang tid å finne en geometrisk sammenheng mellom musikk og matematikk?
Uklang til inspirasjon
Selv om Pytagoras så etter mønstre som klang harmonisk, blir det motsatte brukt bevisst i musikk for å skape enkelte stemninger.
– På grunn av tonesystemet til de gamle grekerne er Europa det eneste området hvor vi har flerstemthet både i folkemusikken og i kunstmusikken. Da europeiske musikktradisjoner møtte de islamske, var det ofte slik at de først sang sine egne sanger, og så gjerne noen av de andre. Denne musikkformen kalles for battaglia-musikk. Da oppsto et behov for å glatte ut rekken med overtoner, for det låt stygt. Før eller siden måtte de forstå hvorfor det låt stygt, og det lar seg forklare med Nyhoffs modell, forklarer Plagge.
Han forteller at battaglia-musikk er årsaken til at vestlig musikk er flerstemt. For at den skal være det og fremdeles høres pen ut, er mange av tonene ikke renstemte. I stedet er nesten alle instrumenter stemt med «temperert stemming». I nyere tid har også musikere tatt i bruk vibrato i musikken.
– Vibrato gjør at vi har en omtrentlighet som overskygger at vi ikke lenger kan høre renstemte toner, sier han. – Vi ofrer skjønnheten i renstemt musikk, men til gjengjeld får vi flerstemthet.
Dersom instrumentene hadde vært renstemte i europeisk musikk, ville de ofte ha møtt på utfordringen med det Pytagoreiske komma. Dette er frekvensområder der noen toner ikke klinger like godt. Ubehagsfølelsen kan brukes til å formidle stemninger som lengsel eller frykt. For dem som vil høre et eksempel på ubehaget disharmonien kan skape, er det bare å lytte til sangen «School» av Nirvana.
– Selv Bach viste systematisk hvordan pianoet skulle stemmes for å forsterke ulike klangopplevelser. På den tiden stemte de gjerne rentonen bittelitt for lys, og da får du en situasjon hvor det skaper spenning, fordi det er en irregularitet der, forklarer Plagge.
I barokken var denne måten å stemme på, en intuitiv forståelse. Nyhoffs forståelse av musikk gjør det mulig å «se» dette fordi det er mulig å lage geometriske konstruksjoner av tonene. Det kan kalles for en geometrisk visualisering av musikken.
– Nå har vi plutselig en modell for hvorfor det oppstår en lengsel i musikken. Begrepet harmoni handler ikke bare om følelser, men også om matematikk, sier Plagge.

De nye kystvaktskipene er levert for lengst – fortsatt store utfordringer
Flere sammenhenger
Musikk er vibrasjoner i luft. Øret vårt kan oppfatte vibrasjoner innenfor et visst intervall. Det vi oppfatter som rene toner, er toner som følger en enkelt sinuskurve. Det finnes mange andre toner også, men disse er satt sammen av ulike sinuskurver. På en måte er øret et avansert matematisk instrument som klarer å oppfatte dette.
Da Pytagoras beskrev oktavene i musikk, klarte han å finne det matematiske forholdstallet mellom klangfulle toner. Forholdstallet er 2:1. Mellom øvre og nedre tone i oktaven kan man regne seg fram til andre toner som klinger godt med disse. I Pytagoras system er disse tallene basert på hele tall. Når et instrument er stemt etter Pytagoras metode, kalles det for «Pytagoreisk stemming».
Problemet med å stemme et instrument etter Pytagoras' metode, er at det er vanskelig å spille en melodi i et annet toneleie – det som på musikkspråket kalles transponering. Når du transponerer, vil noen av tonene få feil som svarer til det Pytagoreiske kommaet, og tonene vil ikke klinge like godt sammen.
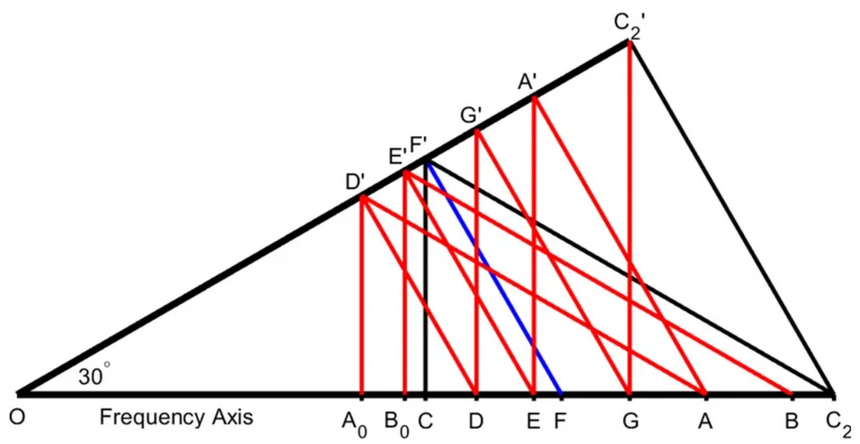
Kan «se» musikk med geometri
For at tonene skal klinge harmonisk, bør instrumentet stemmes slik at hver tone treffer det som lyder pent og at det klinger godt også når du spiller de samme tonene i andre toneleier. Det vil si at en melodi skal klinge like pent om du for eksempel spiller den lysere. Det høres banalt ut, men det er overraskende komplekst.
Hvis du for eksempel skal stemme et piano med den Pytagoreiske metoden, kan du bruke matematikk til å finne ut hvilke toner som skal være med. Problemet er at det ikke er plass til alle tonene. Det er nemlig uendelig mange toner fordi de matematiske frekvensene er en kontinuerlig linje, mens tangentene på pianoet er diskrete. Da oppstår et problem: Hvilke toner skal få lov til å være med i det begrensede utvalget?
Dette har vært en problemstilling musikere har slitt med. I barokken ble problemet løst ved å legge til flere tangenter, men i dag er det vanlig (i vestlig musikk) å dele oktaven i 12 – 7 hele og 5 halve toner. Det gir 88 tangenter i et piano.
Fra 1700-tallet ble det vanligere med temperert stemming. Det er en annen måte å stemme de 88 tangentene på. Det er også mulig å få en såkalt renstemt skala. Den renstemte skalaen følger ikke den pytagoreiske systematisk, men går for enklere tallforhold. Den tempererte skalaen er et kompromiss mellom de to andre.
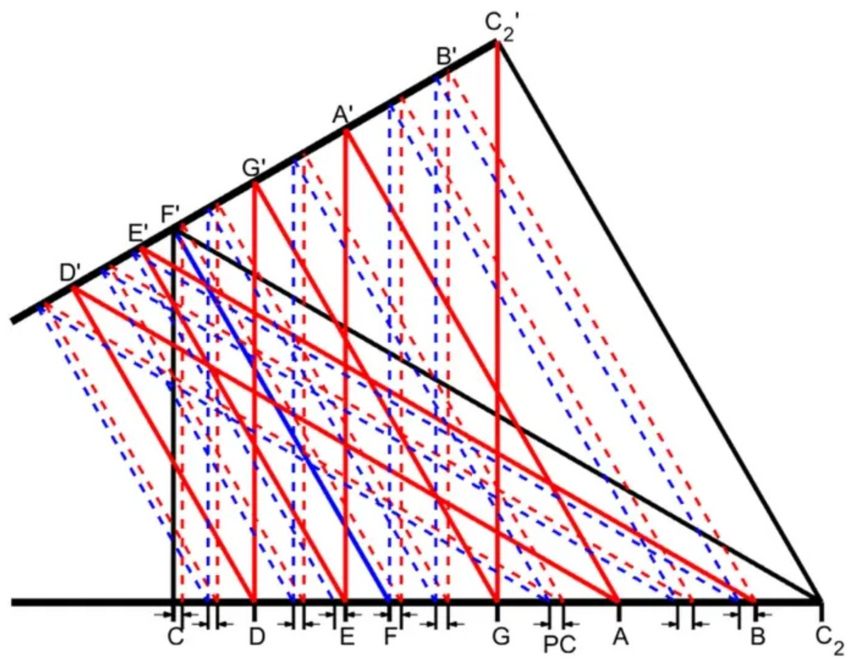
Det finnes fremdeles ingen fasit på hvilke toner som skal være med. Nyhoffs metode gjør det likevel enklere å finne de Pytagoreiske kommaene. Ved hjelp av geometri er det nå mulig å «se» de ulike toneskalaene og områdene der disharmonier dukker opp. Metoden tar utgangspunkt i en ren tone og konstruerer en rettvinklet trekant ut ifra denne.
Selv om arbeidet er minst like interessant innenfor musikkteori, ble det publisert i et matematisk tidsskrift.
Artikkelen ble først publisert på Titan.uio.no

Nye sluser vil sluke minst seks milliarder








